Περιεχόμενα
Σε αυτή τη δημοσίευση, θα εξετάσουμε ένα από τα κύρια θεωρήματα στη θεωρία των ακεραίων - Το μικρό θεώρημα του Φερμάπήρε το όνομά του από τον Γάλλο μαθηματικό Pierre de Fermat. Θα αναλύσουμε επίσης ένα παράδειγμα επίλυσης του προβλήματος για την εμπέδωση του παρουσιαζόμενου υλικού.
Δήλωση του θεωρήματος
1. Αρχικό
If p είναι πρώτος αριθμός a είναι ένας ακέραιος που δεν διαιρείται με pτότε ap-1 - 1 διαιρούμενο με p.
Επισήμως γράφεται ως εξής: ap-1 ≡ 1 (κατά p).
Σημείωση: Ένας πρώτος αριθμός είναι ένας φυσικός αριθμός που διαιρείται μόνο με XNUMX και τον εαυτό του χωρίς υπόλοιπο.
Για παράδειγμα:
- a = 2
- p = 5
- ap-1 - 1 = 25 - 1 - 1 = 24 – 1 = 16 – 1 = 15
- αριθμός 15 διαιρούμενο με 5 χωρίς υπόλοιπο.
2. Εναλλακτική λύση
If p είναι πρώτος αριθμός, a οποιοσδήποτε ακέραιος, λοιπόν ap συγκρίσιμο με a μορφή p.
ap ≡ α (κατά p)
Ιστορικό εύρεσης αποδεικτικών στοιχείων
Ο Pierre de Fermat διατύπωσε το θεώρημα το 1640, αλλά δεν το απέδειξε ο ίδιος. Αργότερα, αυτό έγινε από τον Gottfried Wilhelm Leibniz, έναν Γερμανό φιλόσοφο, λογικό, μαθηματικό κ.λπ. Πιστεύεται ότι είχε ήδη την απόδειξη από το 1683, αν και δεν δημοσιεύτηκε ποτέ. Είναι αξιοσημείωτο ότι ο Leibniz ανακάλυψε ο ίδιος το θεώρημα, μη γνωρίζοντας ότι είχε ήδη διατυπωθεί νωρίτερα.
Η πρώτη απόδειξη του θεωρήματος δημοσιεύτηκε το 1736 και ανήκει στον Ελβετό, Γερμανό και μαθηματικό και μηχανικό, Leonhard Euler. Το Μικρό Θεώρημα του Φερμά είναι μια ειδική περίπτωση του θεωρήματος του Euler.
Παράδειγμα προβλήματος
Βρείτε το υπόλοιπο ενός αριθμού 212 on 12.
Λύση
Ας φανταστούμε έναν αριθμό 212 as 2-211.
11 είναι πρώτος αριθμός, επομένως, με το μικρό θεώρημα του Fermat παίρνουμε:
211 ≡ 2 (κατά 11).
Ως εκ τούτου, 2-211 ≡ 4 (κατά 11).
Ο αριθμός λοιπόν 212 διαιρούμενο με 12 με υπόλοιπο ίσο με 4.










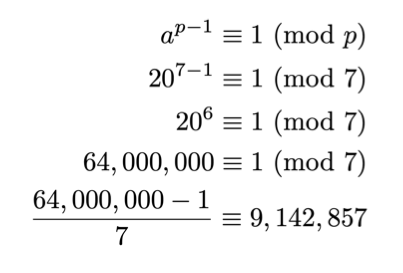
a ile p qarsiliqli sade olmalidir
+ yazilan melumatlar tam basa dusulmur. ingilis dilinden duzgun tercume olunmayib